圆方树

概念

圆方树是一种解决点双、割点有关问题的利器。

在圆方树中，原来的每个点对应一个圆点，每一个点双对应一个方点。
所以共有 $n+c$ 个点，其中 $n$ 是原图点数，$c$ 是原图点双连通分量的个数。
而对于每一个点双连通分量，它对应的方点向这个点双连通分量中的每个点连边。
每个点双形成一个“菊花图”，多个“菊花图”通过原图中的割点连接在一起（因为点双的分隔点是割点）。

显然，圆方树中每条边连接一个圆点和一个方点。

下面有一张图，来自 WC 的 PPT，显示了一张图对应的点双和圆方树形态。

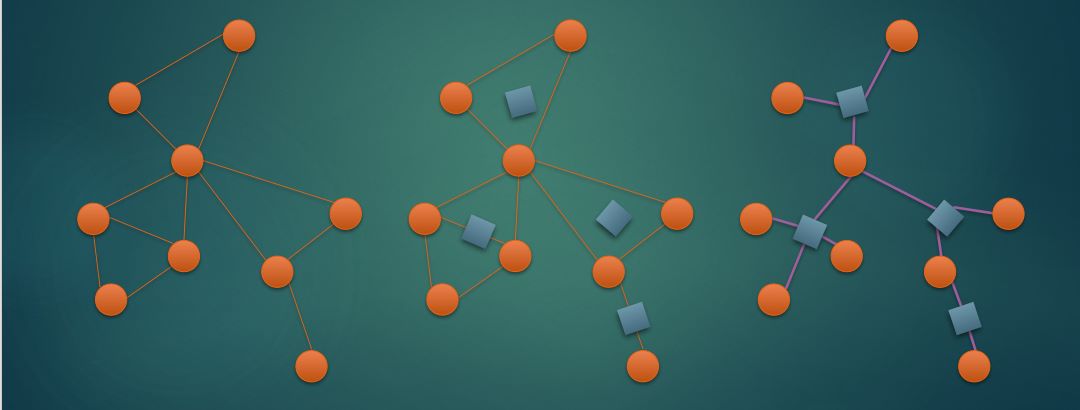
圆方树点数小于 $2n$ ，这是因为原图中割点的数量小于 $n$ ，所以
数组记得开两倍！
另外，若原图不连通，生成的将是一个由“连通分量”个数棵圆方树组成的森林。
如果原图中某个连通分量只有一个点，还需具体情况具体分析。

建树

由于是对每个点双建虚电，考虑 $tarjan$ 求点双。
具体修改不大，只需将原本“标记点双”操作改为“加边”即可。
$\texttt{code}$

int tot;//tot表示树中的点数，需赋初值为n
vector<int> g[100010], t[200010];//g为原图中的边，t为生成的圆方树的树边
stack<int> s;
void tarjan(int p, int fa) {
    dfn[p] = low[p] = ++idx, s.push(p);
    for (auto i : g[p])
        if (!dfn[i]) {
            tarjan(i, p), low[p] = min(low[p], low[i]);
            if (low[i] == dfn[p]) {
                t[++tot].push_back(p), t[p].push_back(tot);
                while (s.top() != i) {
                    t[tot].push_back(s.top());
                    t[s.top()].push_back(tot);
                    s.pop();
                }
                t[tot].push_back(i), t[i].push_back(tot);
                s.pop();
            }
        } else
            low[p] = min(low[p], dfn[i]);
}

用法

类似虚树，圆方树的具体使用视情况而定。

洛谷P5058 [ZJOI2004]嗅探器$\tiny\text{稍微有点没必要}$

题意为求出路径 $(a,b)$ 上经过的编号最小的割点（不包括两端点）。
我们发现圆方树有以下性质：
所有度大于一的圆点（即所有非叶子节点）都是割点（因为有且只有割点处于多个点双）
因此题意可化为求圆方树上两点间编号最小的节点（因为方点编号都大于 $n$ ）。
由于只有一组询问，直接遍历树即可。
若有多组询问可考虑倍增。

$\texttt{code}$

#include <bits/stdc++.h>
#define pb push_back
using namespace std;
int n, dfn[200010], low[200010], idx, tot;
bool used[400010];
vector<int> g[200010], t[400010];
stack<int> s;
int u, v;
void dfs(int p, int fa) {
    int son = 0;
    dfn[p] = low[p] = ++idx, s.push(p);
    for (auto i : g[p]) {
        if (!dfn[i]) {
            dfs(i, p), low[p] = min(low[p], low[i]), son++;
            if (low[i] == dfn[p]) {
                t[++tot].pb(p), t[p].pb(tot);
                while (s.top() != i)
                    t[tot].pb(s.top()), t[s.top()].pb(tot), s.pop();
                t[tot].pb(i), t[i].pb(tot), s.pop();
            }
        } else
            low[p] = min(low[p], dfn[i]);
    }
}
void work(int p, int fa, int dis) {
    used[p] = true;
    for (auto i : t[p])
        if (!used[i])
            if (i == v)
                printf(dis == n ? "No solution\n" : "%d\n", dis);
            else
                work(i, p, min(dis, i));
}
int main() {
    scanf("%d", &n), tot = n;
    while (~scanf("%d%d", &u, &v) && u) g[u].pb(v), g[v].pb(u);
    scanf("%d%d", &u, &v), dfs(u, 0), work(u, 0, n);
    return 0;
}

洛谷P4630 [APIO2018] 铁人两项

给圆方树上节点赋点权以解决统计类问题的板子。

确定 $s,f$ 后，可选的 $c$ 为所有路径可经过点集的并。
在图上不易统计，因此搬到圆方树上。

观察后，我们发现一种可行的赋点权方案是给所有方点赋它周围的圆点数（即点双大小），圆点赋-1。
由于路径上每个点双中任意一点均可选，而割点会被算重，且两端点不可选，故此方法是完全正确的。

此时便可以处理单点的贡献了，为经过此点的路径数乘上点权。由于 $s,f$ 不确定，记得路径数乘二。

PS: 答案要开 long long！

$\texttt{code}$

#include <bits/stdc++.h>
using namespace std;
int n, m, dfn[500010], low[500010], idx, tot, num;
int a[1000010];
long long ans;
vector<int> g[500010], t[1000010];
stack<int> s;
void dfs(int p, int fa) {
    dfn[p] = low[p] = ++idx, s.push(p), num++;
    for (auto i : g[p])
        if (!dfn[i]) {
            dfs(i, p), low[p] = min(low[p], low[i]);
            if (low[i] >= dfn[p]) {
                t[++tot].push_back(p), t[p].push_back(tot);
                a[tot] = 1;
                int pre = 0;
                while (pre != i)
                    pre = s.top(), t[tot].push_back(pre),
                    s.pop(), t[pre].push_back(tot), a[tot]++;
            }
        } else
            low[p] = min(low[p], dfn[i]);
}
int sz[1000010];
void work(int p, int fa) {
    sz[p] = (p <= n);
    for (auto i : t[p])
        if (i != fa) {
            work(i, p);
            ans += 2ll * a[p] * sz[p] * sz[i];
            sz[p] += sz[i];
        }
    ans += 2ll * a[p] * sz[p] * (num - sz[p]);
}
int main() {
    scanf("%d%d", &n, &m), tot = n;
    while (m--) {
        int x, y;
        scanf("%d%d", &x, &y);
        if (x != y)
            g[x].push_back(y), g[y].push_back(x);
    }
    for (int i = 1; i <= n; i++) a[i] = -1;
    for (int i = 1; i <= n; i++)
        !dfn[i] ? (num = 0, dfs(i, 0), work(i, 0)) : void();
    printf("%lld\n", ans);
    return 0;
}