杂题乱做3

CF1503D Flip the Cards

鸽了很久，也攒了挺多题，总之从刚做的开始写。
首先，不能同时有 $a_i\le n,b_i\le n$，因为这样就会存在另一组 $a_j>n,b_j>n$，这两组显然构不成题目中的偏序关系。

钦定原序列中 $a_i,b_i$ 中较小的为 $c_i$，较大的为 $d_i$，我们发现答案序列肯定是一个前缀 $k$ 对所有 $1\le i\le k$ 满足交换后 $a_i\le n,b_i>n$，对所有 $k<i\le n$ 满足 $a_i>n,b_i\le n$，即 $c$ 序列单峰， $d$ 序列单谷。
考虑将原序列按 $c$ 升序排序，答案序列相当于将这个序列撕成两个按 $d$ 降序的子序列，再拼起来。

此时应该可以一车 $\log$ 用 ds 优化 dp 了，但是有优秀而好写的线性做法。我们对排序后的 $d$ 序列做前缀 $\min$ 和后缀 $\max$，如果存在 $\min\limits_{i=1}^kd_i>\max\limits_{j=k+1}^nd_j$，则前后两个部分互不干扰，因此我们将这样的段分开来做。然后，我声称这样的段划分方案是唯一的，因此直接划分，然后分类讨论分成的哪一段翻转即可，写法非常简单。

关于为什么是唯一的：
假设分出的一段是 $[l,r]$，则 $d_l$ 一定不是区间 $\max$，不然会单独划分为另一段。假设区间 $\max$ 的位置为 $m$，如果区间合法，则 $[l,m)$ 区间必然满足 $d$ 单调递减，且划分时这些必然都划分到 $l$ 所在的一段。
若 $m$ 不为 $r$，我们的划分保证存在 $m<n\le r$ 使得 $d_{m-1}<d_n$，因此区间 $[m,n]$ 内所有 $d_i\ge d_n$ 的 $i$ 都选入 $m$ 序列，其余选入 $l$ 序列。
然后我们发现刚才的性质可以继续扩展，即：若 $n<r$，则存在 $p$ 使得 $d_p>\min\limits_{i=l}^nd_i$，因此区间 $[n,p]$ 内所有 $d_i\ge d_p$ 的 $i$ 都选入 $m$ 序列……
于是我们发现划分方案是唯一的。

$\texttt{code}$

CF1500C Matrix Sorting

首先先给行之间两两匹配，可以使用哈希解决，有多个相同的从上至下匹配，如果无法匹配说明无解。
然后，全局排好序相当于 $n-1$ 对相邻行的上下关系都满足，因此我们一组一组考虑。
观察到每一列至多操作一次，所有对于每一组，我们考虑每一列对其关系的影响，如果 $b_{i,j}<b_{i+1,j}$，那么按第 $j$ 列排序后可以修正第 $i$ 组的关系，我们从第 $j$ 列向第 $i$ 组关系连边。若 $b_{i,j}>b_{i+1,j}$，那么按第 $j$ 列排序会打乱第 $i$ 组关系，我们从第 $i$ 组关系向第 $j$ 列连边。然后，这张图的拓扑序状物的倒序就是一组解，特别的，因为只要有一列能修正第 $i$ 组关系就能将其排好序，因此我们将组的入度设为 $1$。
最后，如果一组入读没有清零（即没有列将其还原），一开始也不满足，则无解。

$\texttt{code}$

P6900 [ICPC2014 WF] Sensor Network

（2023.11.29 模拟赛T1）
首先点对之间的距离只有 $O(n^2)$ 个，我们枚举作为答案的点对，记录其距离 $l$。然后枚举哪些点到这两个点的距离都小于等于 $l$，并按在其连线段的哪一侧（叉积的符号）划分。

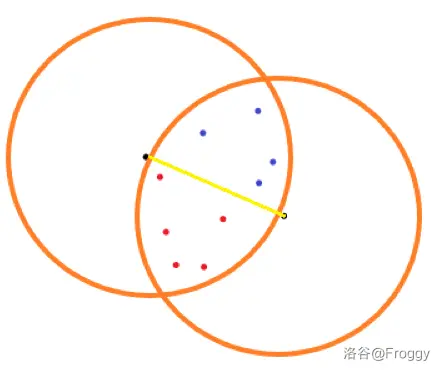
然后在已选的距离大于 $l$ 的点之间连边，观察到同侧的点两两之间距离一定小于等于 $l$，因此连出的是一张二分图，跑最大独立集即可。时间复杂度 $O(n^2\times (n^2 \sqrt n))=O(n^{4.5})$。因为跑不满（枚举点对、最大独立集都是），所以还是跑得比较快的。
补充一下，二分图最大独立集输出方案时，是 A 点集里和源点联通的，以及 B 点集里和源点不连通的。这题还要记得特判 1。

$\texttt{code}$

P7372 [COCI2018-2019#4] Slagalica

（2023.11.28 模拟赛T3）
感觉评不了黑。首先，我们发现 T x y R x y R x y 三步可以交换 (x+1,y) 和 (x+1,y+1)。然后，通过将想交换的两个转到菱形上方，我们得到了交换任意邻项两个的方法。因此我们学会了构造任意大小的环。于是将 $k$ 分解质因数，然后将 $nm$ 个点划分成组，分别对应 $k$ 每个质因数的最高次幂即可。

$\texttt{code}$

P5037 抓捕

没怎么写过点权最短路就写了下。简单题，注意到点权最短路中一个点第一次被访问到时就是最优方案，因此当松弛时直接判一个点是否被访问过即可，单次最短路的复杂度为 $O(n \log n + m)$。

$\texttt{code}$

P8518 [IOI2021] 分糖果

（2023.11.24 模拟赛）
扫描线对每盒糖果单独做，将区间操作转化为时间上的后缀加。

$\texttt{code}$

CF1515F Phoenix and Earthquake

感觉挺神秘的，，不是很会这种题。。
结论是随便构造一棵生成树，只要 $sum_{a_i}\le k\times(n-1)$ 就一定有解。
构造方法是从叶子往根做，如果一个叶子 $i$ 的 $a_i\ge k$，那么直接合并，剩下的部分依然满足性质；否则放到最后做这个，相当于砍掉这个叶子，砍掉了一个节点但值减少不到 $k$，依然满足性质；并且最后合并时一定合法，这是由 $sum$ 保证的。
因此构造长度 $n-1$ 的答案序列，随便 $dfs$ 生成树，叶子大于等于 $k$ 就加上其权值 $-k$ 并放在答案序列前面，否则放在后面。

$\texttt{code}$

[ARC080F] Prime Flip

首先，做差分，区间修改转化为修改两点。若差分后有奇数个点直接无解。
否则，任意两点之间都能够互相抵消。具体的：

• 差为奇质数：1步
• 差为偶数：2步
• 差为奇数合数：3步

解释下差为偶数为什么是 2 步：
差为 2 时，5-3=2；差为 4 时，7-3=4；否则，由哥德巴赫猜想在 $10^7$ 以内的正确性易得。

然后，我们先在差为奇质数的点之间连边，观察到这是张二分图：奇数连偶数。然后跑最大匹配，最后两边先尝试 2 步的，如果还剩下一对则 3 步。

$\texttt{code}$

CF794D Labelling Cities

值一样的点能到点的集合（包括自身）必定一样，所以我们异或哈希，将能到点集合一样的点缩到一起。
然后发现这样缩完点之后如果合法，原图必定缩成了一条链，因此判链，直接按链的顺序赋值就好了。

$\texttt{code}$

CF1375F Integer Game

好玩题。假定三个数为 $a,b,c$，大小不重要。
第一步，加 $\inf$，假设加了的是 $c$，变为 $a,b,c+\inf$。
第二步，加 $2c-a-b+2\inf$，假设加了的是 $b$，变为 $a,c+\inf,2c-a+2\inf$。
第三步，加 $c-a+\inf$，容易发现此时后手无法操作。
同时我们也发现了先手必胜。

$\texttt{code}$

CF1493E Enormous XOR

首先，如果 $l,r$ 最高为不同，答案必为 $r$ 的位数个 $1$，构造显然。

然后，若位数相同，则必然选奇数个。
我们考虑如下事实：对于任意偶数 $x$ 都满足 $x\oplus(x+1)=1$。
由于我们选奇数个，因此答案相当于一堆 $1$ 异或上一个值。
因此异或上的值必定为 $r$。具体的，若 $r$ 为偶数且 $r-l+1\ge3$，则答案为上 $r\oplus1$，否则为 $r$。

$\texttt{code}$

P8424 [JOI Open 2022] 跷跷板（Seesaw）

首先，一开始所有数的平均数一定在答案区间内。设这个平均数为 $M$。

简单观察后，我们发现一次操作一定是删除最左或最右的一个值。

对于 $n-i$ 次操作后形成的所有长度为 $i$ 的区间，我们找出平均值为 $M$ 前驱的区间 $[l1,r1]$ 和为 $M$ 后继的区间 $[l2,r2]$。可以证明答案的方案中一定选择了这两个区间中的恰好一个，并且这两个区间一定可由长度为 $i+1$ 的两个区间转移得到。

于是我们将相同长度的两个区间的绝对值打包成一个 pair，则答案相当于对这 $n$ 个 pair 每个取一项，使得极差最小。简单贪心即可。

$\texttt{code}$

CF1975G Zimpha Fan Club

虽然可能并不是很难，但是由于我真的几乎没写过需要多项式的题，还是写写 sol 吧。

对于两个字符串都没有 * 的情况，直接按位比较即可。对于都有 * 的情况，比较都没有 * 的一段前驱和一段后继即可，可以证明中间总能匹配上。

现在假设字符串 $s$ 中没有 *，字符串 $t$ 中有 *。先在 $s$ 中匹配 $t$ 中没有 * 的前驱和后继，然后将其删去。接下来即可将 $t$ 通过 * 划分成若干小字符串。我们可以从前往后贪心地匹配这些小字符串，通过能否匹配完判断是否有解。

于是，问题转化为了：要在长为 $n$ 的字符串 $s$ 中求出长为 $m$ 的字符串 $t$ 最早的出现位置。

由于有通配符，不能使用哈希或是 kmp 之类的方式。事实上，这是一个经典问题，可以通过 fft 来解决：

• 构造 $f_i=\sum\limits_{j=0}^{m-1}[a_{i+j}\ne 0][b_j\ne 0](a_{i+j}-b_j)^2$，其中

$$a_i=\begin{cases} 0 ,& s_i\text{为通配符} \\ s_i ,& \text{otherwise.} \end{cases}$$

$$b_i=\begin{cases} 0 ,& t_i\text{为通配符} \\ t_i ,& \text{otherwise.} \end{cases}$$

• 按照定义，$f_i=0$ 的位置 $i$ 即为匹配上的位置。

• 化开式子： $f_i=\sum\limits_{j=0}^{m-1}[a_{i+j}\ne 0]b_j^2+\sum\limits_{j=0}^{m-1}[b_j\ne 0]a_{i+j}^2-2\times\sum\limits_{j=0}^{m-1}a_{i+j}\times b_j$

三部分均可以使用减法卷积解决，于是，我们在 $n\log n+m\log n$ 的复杂度内完成了一次查找。

然而，这个复杂度是不够优秀的，因为我们可能在 $s$ 中进行 $10^6$ 次匹配。于是乎，我们希望优化掉这个 $n\log n$。

解决方法是：每次只取出 $s$ 的前 $2\times m$ 项进行匹配，如果没匹配上，我们就删除 $s$ 的前 $m$ 个字符。这样我们以 $m\log m$ 的复杂度删除了 $s$ 中一个长度为 $m$ 的字符串。由于 $\sum m$ 得到保证，且 $s$ 被删除总长不超过 $n$，我们就在 $n\log n$ 的复杂度内解决了这个问题。

$\texttt{code}$

P10070 [CCO2023] Travelling Trader

毅力大挑战。。

k=1，选一条 1 为根的链。k=3，能走完所有点，构造是容易的。

k=2，分4种状态，10种转移进行 dp（以下罗列4种状态）：

1. 一开始在 p，不回去
2. 一开始在 p，最后在 p 的儿子（或 p）
3. 一开始在 fa，不回去
4. 一开始在 fa，回到 p

推完转移会发现，转移只需要前后缀 $\max$ 之类的，都是平凡的。

$\texttt{code}$

P10529 [XJTUPC2024] 勘探队

求出每一段的重量 $m$，x轴上的移动距离 $s$，则这一段的代价为 $f(y)=m\times\sqrt{s^2+y^2}$。如果相邻两端导数不同，则稍微调整后可以得到更优的答案，因此最终方案中每一段的导数一定相同。而注意到 $f'(y)=\dfrac{my}{\sqrt{s^2+y^2}}$ 单增，因此可以二分导数，反推每一段的 $y$。

$\texttt{code}$