抽屉原理趣题选讲（一）

前言

本文的灵感源于 cyy 从神秘书籍上找到的三道有趣的抽屉原理例题，题目并不偏难怪，但是需要大家锻炼平常用不到甚至有时被视作“脑筋急转弯”的相关知识。写本文的目的旨在让大家在繁杂的学业中开拓一点思路，感受一点数学的乐趣。
不知道是否有续集故先标上（一）。文章完成时间短，且笔者能力有限，不一定会使用形式化语言规范描述推理过程，或许存在一些逻辑漏洞，欢迎同学指出我的问题，探讨不同（更优）做法，也可以为可能存在的（二）供题。感激不尽。

例题一：象棋训练

题目描述

为了提高自己的象棋水平，小C决定每天下一盘象棋，连下 $T=11$ 周。已知小C在每周内不会下超过 $12$ 盘棋，即小C在第 $1\sim 7$ 天，第 $8\sim 14$ 天，第 $15\sim 21$ 天……内均不会下超过 $12$ 盘。试证明：一定存在连续的某几天内小C恰好下了 $N=21$ 盘。

解法简析

这是 cyy 某天放学前跟我说的题，第二天过来被我爆标了，遂放入 bonus 版本。在此仅讲解官方做法。

以下均记 $a_i\ (1\le i \le 77)$ 表示到第 $i$ 天下完为止已下的盘数，则有： $a_i<a_{i+1}\ (1\le i\le 76)$， $1\le a_i\le 11\times 12=132$。

考虑反证。若不存在一段时间内恰好下了 21 盘，则有：
序列 $a_1,a_2,\dots a_{77},a_1+21,a_2+21\dots a_{77}+21$ 中不存在重复元素。

注意到，序列中任意元素 $x$ 均满足 $1\le x\le 132+21=153$，而序列中有 $2\times 77=154$ 个元素，因而必定有两个相等（抽屉原理）。

思考题

试使用以上方法，证明当 $N=1,2,\dots 20,22$ 时结论是否成立。
当 $N=22$ 时做法稍有不同，但对聪明的你来说一定不足挂齿（）

例题一 bonus

题目描述

基本同上，但 $T=3$ 即证明三周内结论依然成立。

解法简析 1

这是我放学回家灵机一动想到的做法。

类似原题做法，有 $1\le a_i\le 36\ (1\le i\le 21)$ 。

我们有：

1. $a$ 中不同时存在 $1$ 和 $22$， $2$ 和 $23$，……，$15$ 和 $36$
2. 不存在 $a_i=21$ ，否则取第 $1$ 到 $i$ 个即可。

此时注意到 $a_i$ 中只有 $20$ 种可能的不同取值，而 $a_i$ 中有 $21$ 个元素，与假设矛盾，因而反证成功。

解法简析 2

这是我第二天补觉时想出的妙解（）

我们有引理：

对于长度为 $n$ 的正整数序列 $a$ ，一定存在一个非空子串的和为 $n$ 的倍数

一般的，我们认为 子串 表示序列中连续的一段， 子序列 表示序列中任意删去若干个数剩下的部分

这是书上此题前一道例题。证明过程不难，记 $s_i=\sum\limits_{j=1}^i a_j$ ，特别的，记 $s_0=0$ ，则子序列 $a_{l\sim r}$ 的和可以表示为 $s_r-s_{l-1}$ ，由此我们可将目标刻画为证明存在 $s_i\equiv s_j\pmod{n},i\neq j$ 。注意到 $s$ 中下表为 $0\sim n$ 有 $n+1$ 项，因此显然存在。

考虑使用这个结论解决这个问题。我们发现 $21$ 天内必定有一段和 $s$ 是 $21$ 的倍数，并且 $1\le s\le 3\times 12=36< 42=21\times 2$ ！

没看懂吗？有一段和是 $21$ 的倍数，并且比 $21$ 的 $0$ 倍大， $2$ 倍小，因此是 $1$ 倍！真是太神奇了！

例题二：圆盘匹配

题目描述

小C有内外两个圆盘，各被等分为 $200$ 小格。外圆盘恰有 $100$ 被染为红色， $100$ 格被染为蓝色，内圆盘各格子被随机染色。定义内、外圆盘对应小格颜色相同为一对成功匹配。试证明：对于内、外圆盘任意一种染色方案，在内圆盘旋转一周与外圆盘进行匹配的过程中，均存在至少一种方案中存在至少 $100$ 对成功匹配。
提供如下一个小样例供理解题意。在样例中，内外圆盘仅有 $2$ 组成功匹配，但若将内圆盘顺时针旋转一格，将形成 $6$ 组成功匹配。

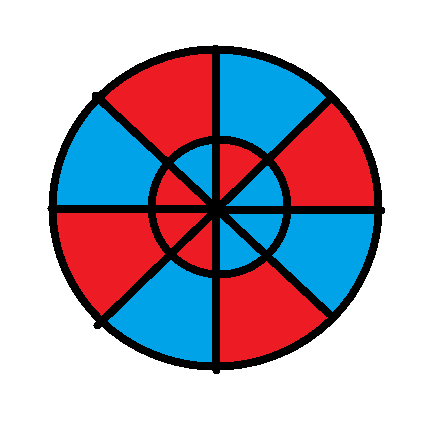
再提供一个 hint， 信息量非常大，谨慎食用：

注意到对于任意可重数集，最大值 $\le$ 平均数（这也是抽屉原理？）

解法简析

hint 差不多说完了。

对于内圆盘的一个色块，不论为何颜色，在旋转的过程中均可形成 $100$ 对成功匹配，即内外圆盘共可形成 $20000$ 对成功匹配，在每个位置上平均形成 $100$ 对成功匹配，利用 hint 结论及可证明。

例题三：排列增减

题目描述

给定一个长为 $n^2+1$ 的排列 $a$ ，证明以下结论中至少有一个成立：

1. 排列中存在一个长为 $n+1$ 的递增（上升）子序列
2. 排列中存在一个长为 $n+1$ 的递减（下降）子序列

长为 $N$ 的排列 的定义为由 $1\sim N$ 这 $N$ 个正整数重排得到的数列。

解法简析

应该是经典题，但我做的时候忘了（

问题等价于证明：

1. 当排列最长上升子序列长度不超过 $n$ 时，最长下降子序列长度至少为 $n+1$ 。
2. 当排列最长下降子序列长度不超过 $n$ 时，最长上升子序列长度至少为 $n+1$ 。

二者证明过程几乎一致，这里仅证明第一个。

记 $l_i$ 表示 以 $i$ 位置为开头 的最长上升子序列。例如：对于排列 $a=\{4,1,3,5,2\}$ ，其对应的 $l=\{2,3,2,1,1\}$ 。

由于最长上升子序列长度不超过 $n$ ，我们有 $1\le l_i\le n$ 。$l$ 中有 $n^2+1$ 个元素，由抽屉原理，我们知道一定存在 $P=\{p_1,p_2,\dots,p_{n+1}\}\ (1\le p_1< p_2<\dots<p_{n+1}\le n^2+1)$ 使得 $l_{p_1}=l_{p_2}=\dots=l_{p_{n+1}}$ 。

显然，当 $i<j$ 且 $a_i<a_j$ 时，一定有 $l_i\ge l_j+1$ 。因此，当 $i<j$ 且 $l_i=l_j$ 时，有 $a_i>a_i$ ，故 $a_{p_1},a_{p_2},\dots,a_{p_{n+1}}$ 构成一个长为 $n-1$ 的递减子序列。

结语

由于笔者能力有限，仅对例题进行了浅显的分析和讲解，缺乏相关的拓展内容（）

希望大家在闲暇时，在繁琐的导数/圆锥曲线计算之余，也可以不忘做做抽屉原理，扫扫雷推推箱子推推数独数织，保持一份对数学本真的热爱（）